數學(四)算珠

數學系列是寫給自己看的，一方面是把哥哥的學習過程記錄下來，二年後帶弟弟學習時可以回顧及修正，內容很摘要；另一方面，我覺得數學是一門非常很有趣的學問，自己從小到大的數學成績都還不錯，我希望藉由育兒的過程，觀察小兒對於數學的反應，重新醒思數學的發想過程，也許能夠找出在學習數學上更有效率的關鍵點，這也會是人生很難得的體驗。

因為哥哥才三歲多，我看他應該也不像是網路上看到那些很不平凡的天才，如果沒有藉助一些實體的東西輔助可能就只是簡單帶過這段過程，於是選擇了算珠當成玩具兼教具，在遊戲的過程中希望剛萌芽的火花不要熄滅，當然能夠越燒越旺就太好了。

算珠

依照算珠的數量可區分為：傳統一上四下的算盤、傳統一上五下的算盤、傳統上二下五的算盤(好像可以用來算斤，算到15)；九珠算盤、十珠算盤。

九珠算盤再依顏色可分為單色、雙色、三色。

十珠算盤則依顏色可分為單色、雙色、三色。

三歲多的兒童對於數學的認識，除了多、少、前、後、左、右這樣的相對觀念，其餘都要靠實物來引導，沒有辦法直接用心像作更深入的應用，有很多種教具可以選擇，例如：積木堆疊、雙色進位積木、

數粒、數棒、算珠…，為了銜接未來小學數學課程，我選擇了十珠算盤，以1為單位，進行基本且直覺的運算。

十珠算盤的好處是直觀，不需口訣，用一個小算盤就可以算一百的數，另外，因為直接用量的觀點進行計算，所以加、減、乘、除甚至有些應用都可以在算珠的移動中體會出來。

缺點就是日後轉為直式時，在進位的學習上會稍微卡一下，九珠的進位就比較接近直式，但進位這個部份我覺得倒還好，等到有區分出個、十、百、千、萬位數的觀念，自然就通了。

為什麼選擇雙色算珠，而不是單色算珠？

根據百力數學部落格裡面的教學經驗指出，採用單色十珠教學後，對於大班的成效較傳統教學方式佳，但對於中班甚或小班的小朋友來說，效果就沒有大班的顯著，或許是十珠數量較多，較小的小孩無法產生數感，改為以五為單位的雙珠效果就很好，因為我是從三歲半開始教，所以我選擇雙色來引導，本以為5+1=6這樣的表達會很抽象，從哥哥的表現看來，接觸幾天就可以直觀的撥出。

利用算珠建立數感 不用手指計算

因為小孩還沒有足夠的量感，沒有辦法在腦中產生圖像以供應用，因此要藉助實物來輔助，坊間的心算班也是要先靠實體的算盤或是紙算盤，經過充分練習後產生直覺，才可以進行腦海中產生虛擬圖像。    

手指最多只能進行到二十以內的計算，而普通程度的小孩只能用手指算十以內的和，不夠還要用到腳，一樣要學計算，一樣只是過渡的工具，我選擇較用途較多的輔具。

不選擇算珠可行嗎？

如果說數學是科學之母，那麼計算絕對是數學最基礎中的基礎，當然基本數學包含：計算、數、量、空間、幾何、邏輯…不過，經由計算的反覆練習，可以硺磨出許多數學的關鍵能力，數學要好，計算能力一定要好，當思考「二隻牛和五隻雞總共幾隻腳？」時，如果基本的佈式就列不出來，加上計算也是哩哩啦啦，整個過程就被會卡住了，沒有成就感，怎麼可能學得好！

計算有很多種練習法，最終的目的只通向一個結果----可以準確而迅速的算出答案，如果不是藉由工具，那麼就要利用內心運算，算珠並非唯一的途徑，也並非最好的途徑，但在家慢慢地教小孩，我覺得這是很適合的輔助工具。

我們不學珠心算

數學是全世界約定成俗的語言，用來將這個世界的細節用抽象的語言進行描述，比如說：北回歸線是北緯23.5°，如果沒有定義出北，定義出緯度的意義，那麼就無法進行有效率的溝通，珠心算專注的部份是計算速度及精確度，額外增加的價值是大腦能力的強化，以我唸到大學時的觀察，雖然我們系上的學生都是大學聯考數學超高標，但心珠算在班上同學身上並沒有特殊的影響，以前大學考試時三個小時要寫完四道統計題目，還是open book，沒帶工程計算就糗了，計算是項工具，但邏輯、應用也都是很重要的一環。

因此珠心算如果要學，學到上段，有基本的計算能力來輔助應用題的解題速度就已足夠，可以讓數學的學習更有樂趣，有心向上突破的再進行更進階的珠心算訓練。

算珠終舊只是個工具，最終還是要回歸到能夠以心計算，我希望我家小孩上小學時不要害怕數字，對數學能夠有興趣這樣就好了。

另一個問題是，算珠的解構方法與坊間的珠心算方法不見得相同，同時學兩套系統也許會造成兒童混洧，進而無法達到預期的目標，這樣反而會得不償失。

不論是積木、珠心算、算珠等，都是藉由實體操作的過程，去體悟數感的形成，因此，可以強化記憶、思考、圖像運用的心像能力；這是藉由反覆筆算(指直式練習)或是計算機輔助所無法達到的練習，準確的結果固然很重要，過程中經歷的點點滴滴也都不知不覺中影響了其他面向。

另一個很重要的思考重點，就是我家太鄉下了，附近沒有珠心算班……

算珠可以把想法具體化 

雖然有些父母覺得學校要求要寫3*5，為什麼不可以寫成5*3，覺得這樣很龜毛，但我想舉一個例子：

如果有五台三輪車，總共有幾個輪子？

列式是3*5還是5*3？

 

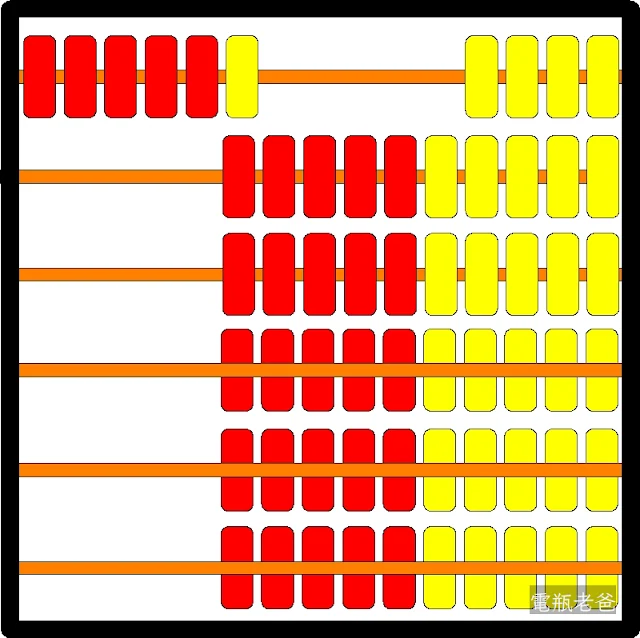
如果從算珠上來看

5*3是

 3*5是

 那張圖才是合理的呢？

雖然兩種解法都可以說得通，但在【在國小】初學乘法概念時，這題的答案應該是3*5=15(個)，如果要取巧一點的方式，就是教小孩，題目是問輪子，在列式時就把輪子放在前面，但這終究不是正道啊！

在實務上，3*5=15與5*3=15在單位的化整後是相等的，並無差異，而3+3+3+3+3=3*5則是國小課程中想要傳達乘法的觀念，因此低年級階段會嚴格要求要會寫出3*5，才可知道是否真的瞭解解乘法的意義。

想到一個以前聽過的故事，有一個小孩，三歲多就會從一數到一百，也會十以內的加法，大家都說他未來會是個神童。

結果到了國小五年級，

也只會從一數到一百，只會簡單的加法，數學成績是班上的倒數……